Yet Another Scheme Tutorial

发表于 2022-06-08 分类于翻译稿本文字数： 8.1k

原文：http://www.shido.info/lisp/idx_scm_e.html

该教程目的之一是提供足够 Scheme 语言相关背景知识以方便阅读 SICP

第一章 - 安装MIT-Scheme

为何学习Scheme

学习Scheme, 你可以：

编写漂亮的程序
享受编程的乐趣

这就是学习 Scheme 唯一的两大好处了，如果用它编写实用程序则会遇到很多实际困难

比起 Lisp，Scheme 有：

更紧凑的语言设计
更简单的语法

Scheme 程序只包含单词，小括号和空格。它的括号规模可能让初学者望而却步，不过一个合适的编辑器即可解决。

安装MIT-Scheme

Scheme 有很多语言标准，最新的是Revised5 Report on the Algorithmic Language Scheme (R5RS)，大多 Scheme 实现都（完整或部分地）基于 R5RS

Windows 有很多可用的 Scheme 实现，本教程使用MIT/GNU Scheme，因为它易于安装并且性能也足够好，并可以编译出本地代码（native code），缺点是不完全满足 R5RS，教程中，遇到（不满足 R5RS 的地方）会给出说明。

如何在 Windows 安装MIT-Scheme

仅需下载安装器并执行即可：

~~访问the homepage of MIT/GNU Scheme下载 Windows 安装器~~（译注：最新版 MIT-Scheme 已不支持Windows，可访问 https://ftp.gnu.org/gnu/mit-scheme/stable.pkg/9.2/ 下载旧版）
双击安装器，执行默认安装
编辑 %HOMEPATH%/scheme.init 可以配置安装好的MIT-Scheme，示例：

1 2	(cd "C:\\doc\\scheme") (define call/cc call-with-current-continuation)

除了配置scheme.ini，MIT-Scheme的安装是很简单的，下一章将学习如何和 Scheme 前端交互。

第二章 - 将 Scheme 作为计算器使用

介绍

如果将 Scheme 作为计算器使用，它将比 Windows 自带计算器更强大

将 Scheme 作为计算器使用

从开始菜单打开 Scheme 解释器，输入：(+ 1 2)

1 ]=> (+ 1 2)

;Value: 3

1 ]=>

注意以下三点：

一对小括号表示一步运算。本例：(+ 1 2) 表示步骤 1+2
左括号后为函数名，紧接着是参数，Scheme 大多数运算符都是函数。本例，’+’是函数，1, 2是参数
空格、制表符、换行符是各种符号间的分隔符

求值的方式与其他语言函数调用 +(1, 2) 是相同的，先对参数求值（参数求值顺序未规定），再求本次运算的值
细节：

首先，’+’符号被求值为加法函数，’1’被求值为1，’2’被求值为2
最后，3从 (+ 1 2) 中计算出来

‘+’ 接收任意多个参数

(+) → 0
(+ 1) → 1
(+ 1 2) → 3
(+ 1 2 3) → 6

四种基本运算

Scheme 可以处理小数，exact->inexact函数将小数转换为浮点数。Scheme也可以处理复数，复数的表示形式为 a+bi, ‘+’, ‘-‘, ‘*’, ‘/‘ 代表加减乘除四种基本运算，它们（函数）都可以接收任意多个参数

(- 10 3) → 7
(- 10 3 5)  → 2
(* 2 3) → 6
(* 2 3 4) → 24
(/ 29 3) → 29/3
(/ 29 3 7) → 29/21
(/ 9 6) → 3/2
(exact->inexact (/ 29 3 7)) → 1.380952380952381
(* (+ 2 3) (- 5 3)) → 10
(/ (+ 9 1) (+ 2 3)) → 2

包含括号，符号，分隔符的公式称为S表达式

练习1

使用 Scheme 解释器计算如下式子：

(1+39) (53-45)
(1020 / 39) + (45 2)
Sum of 39, 48, 72, 23, and 91
Average of 39, 48, 72, 23, and 91 as a floating point.

其他算术运算符

商、余数、取模、开方

函数 quotient 用于取得商
函数 remainder，modulo 用于取得余数
函数 sqrt 用于计算参数的平方根

1
2
3

(quotient 7 3) → 2
(modulo 7 3) → 1
(sqrt 8) → 2.8284271247461903

三角函数

Scheme 提供 sin, cos, tan, asin, acos, atan 计算三角函数的值，atan 接受一个或两个参数，两个参数的形式在其他语言中又叫atan2

1 2	(atan 1) → 0.7853981633974483 (atan 1 0) → 1.5707963267948966

幂和对数

使用 exp 和 log 计算幂和对数，a的 b 次方写作(expt a b)

练习2

使用 Scheme 解释器计算如下式子：

circle ratio, π
exp(2/3)
3 to the power of 4
logarithm of 1000

总结

本章将 Scheme 解释器当做计算器使用，下一章将介绍列表数据类型

练习答案

练习1

;1
(* (+ 1 39) (- 53 45))              ⇒    320

;2
(+ (/ 1020 39) (* 45 2))            ⇒    1510/13

;3
(+ 39 48 72 23 91)                  ⇒    273

;4
(exact->inexact (/ (+ 39 48 72 23 91) 5))   ⇒    54.6

练习2

;1
(* 4 (atan 1.0))          ⇒   3.141592653589793

;2
(exp 2/3)                 ⇒   1.9477340410546757

;3
(expt 3 4)                ⇒   81

;4
(log 1000)                ⇒   6.907755278982137

第三章 - 列表

由于 Scheme 是 Lisp 的一种方言，它很善于操作列表。同时，列表是一个重要概念，需要对列表有充分的理解，才能掌握 Scheme

在递归函数和高阶函数中，列表担任相当重要的角色，这些将在后面的章节出现

本章，介绍一些基本的列表操作符，例如：cons，car，cdr，list，和quote

Cons Cells与列表

Cons Cells

cons cells是列表的组成部分，它是一段存储了两个地址的内存区域，可以用 cons 函数创建cons cells

在解释器输入(cons 1 2)

1 2	(cons 1 2) ;Value 11: (1 . 2)

它输出(1 . 2)。如下图，cons（construction的缩写）函数分配存储两个地址的内存空间，将数据 1 的地址存放在名为 car（Contents of the Address part of the Register的缩写）的部分，将数据 2 的地址存储在名为 cdr（Contents of the Decrement part of the Register的缩写）的部分（译注：后文简写为 cdr 部，同样，car 部分简写为 car 部），car 和 cdr 源自最初的 Lisp 机硬件。

fig1

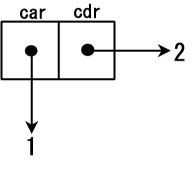
cons cells可以串联起来

1 2	(cons 3 (cons 1 2)) ;Value 15: (3 1 . 2)

(3 1 . 2) 是 (3 . (1 . 2)) 的简便写法，这种情况下，它创建的内存空间如下图所示：

fig2

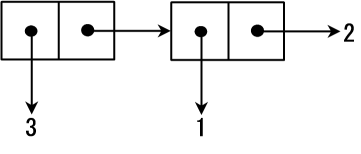
cons cells可以嵌套，并且可以存储不同种类的数据

(cons #\a (cons 3 "hello"))
;Value 17: (#\a 3 . "hello")

(cons (cons 0 1) (cons 2 3))
;Value 23: ((0 . 1) 2 . 3)

这是因为 Scheme 通过地址操作所有数据。上面的例子中，#\a 代表字符 a

Lists

列表是串联的 cons cells，其最后一个 cons cell 的 cdr 部为 '()（空列表），也包含在列表中，下图展示列表 (1 2 3) 的内存布局

fig3

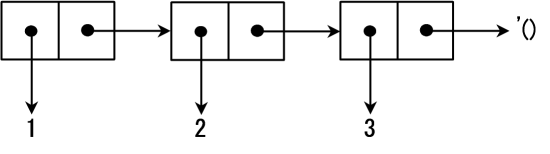
实际上，列表可以递归地定义

'() 是一个列表
如果 ls 是一个列表，obj 是某种数据，则 (cons obj ls) 是一个列表

由于列表可递归地定义，递归函数使用列表就很自然了

Atoms

不使用 cons cells 的数据结构称为 atoms，数字、字符、字符串、向量、以及 '() 都是 atoms，'() 同时也是一个列表

练习1

使用 cons 创建数据结构，使解释器产生如下输出：

(“hi” . “everybody”)
(0)
(1 10 . 100)
(1 10 100)
(#\I “saw” 3 “girls”)
(“Sum of” (1 2 3 4) “is” 10)

quote

Scheme 的求值顺序是从内层括号一直向外的，S表达式每个符号都无一例外的被求值

quote 可以用来防止符号被求值，如 (+ 2 3) 的值是 5，而 (quote (+ 2 3)) 的值为列表 (+ 2 3)

考虑到 quote 使用的频繁性，可以用一个引号代替书写 quote

‘(+ 2 3) 即列表 (+ 2 3) 本身
‘+ 即符号 + 本身

特殊形式

Scheme 有两种运算符，其一是函数，函数对所有参数求值，然后得到一个值。另一种是特殊形式，它们不求值所有参数，除 quote 外，lambda，define，if，set!等都是特殊形式

car函数、cdr函数

car函数、cdr函数分别返回 cons cells 的 car 部和 cdr 部。~~如果 cdr 部是串联的 cons cells，解释器输出 car 部整个值；如果最后一个 cons cell 的 cdr 部不是 ‘()，它的值也会输出在 . 后面。~~(译注：不太理解这句话)

(car '(1 2 3 4))
;Value: 1

(cdr '(1 2 3 4))
;Value 18: (2 3 4)

练习2

计算如下S表达式：

(car ‘(0))
(cdr ‘(0))
(car ‘((1 2 3) (4 5 6)))
(cdr ‘(1 2 3 . 4))
(cdr (cons 3 (cons 2 (cons 1 ‘()))))

list函数

list函数创建一个包含多个元素的列表

(list)
;Value: ()

(list 1)
;Value 24: (1)

(list '(1 2) '(3 4))
;Value 25: ((1 2) (3 4))

(list 0)
;Value 26: (0)

(list 1 2)
;Value 27: (1 2)

总结

本章介绍了列表以及列表的基本操作，本章及以前的章节或许比较枯燥，下一章可能会有意思一些，下章内容将包括：

如何使用编辑器编写代码
如何加载代码至解释器
如何定义函数

练习答案

练习1

;1
(cons "hi" "everybody")
;Value 32: ("hi" . "everybody")

;2
(cons 0 '())
;Value 33: (0)

;3
(cons 1 (cons 10 100))
;Value 34: (1 10 . 100)

;4
(cons 1 (cons 10 (cons 100 '())))
;Value 35: (1 10 100)

;5
(cons #\I (cons "saw" (cons 3 (cons "girls" '()))))
;Value 36: (#\I "saw" 3 "girls")

;6
(cons "Sum of" (cons (cons 1 (cons 2 (cons 3 (cons 4 '())))) (cons "is" (cons 10 '()))))
;Value 37: ("Sum of" (1 2 3 4) "is" 10)

练习2

;1
(car '(0))
;Value: 0

;2
(cdr '(0))
;Value: ()

;3
(car '((1 2 3) (4 5 6)))
;Value 28: (1 2 3)

;4
(cdr '(1 2 3 . 4))
;Value 29: (2 3 . 4)

;5
(cdr (cons 3 (cons 2 (cons 1 '()))))
;Value 31: (2 1)

第四章 - 定义函数

到这里，我们已经学习了：

如何安装MIT-Scheme
S表达式的求值方法
列表基本操作

本章，将讲解如何定义自己的函数，作为一门函数式语言，程序就是由我们编写的一个个小函数构成的。因此，理解如何定义和组合函数相当关键。

鉴于在解释器定义函数有诸多不便，所以我们一般在编辑器写好函数，然后将其加载进解释器执行。

定义简单函数并加载执行

使用 define 为值指定一个符号

使用任一编辑器编辑并保存如下代码为 hello.scm

; Hello world as a variable
(define vhello "Hello world")     ;1

; Hello world as a function
(define fhello (lambda ()         ;2
		 "Hello world"))

然后，在解释器执行：

(cd "C:\\doc\\scheme") ; 将 C:\\doc\\scheme 换成保存 hello.scm 的地方
;Value 14: #[pathname 14 "c:\\doc\\scheme\\"]

(load "hello.scm")
;Loading "hello.scm" -- done
;Value: fhello

这样，hello.scm就被解释器载入了，然后，在解释器运行：

vhello
;Value 15: "Hello world"

fhello
;Value 16: #[compound-procedure 16 fhello]

(fhello)
;Value 17: "Hello world"

define 是用来定义变量的操作符，它接收两个参数

该操作符要求将第一个参数作为全局参数，并将它绑定给第二个参数。于是，hello.scm ;1 标注的地方定义了一个全局参数并绑定至”Hello World”，同样，;2 标注的地方定义了一个函数，它返回”Hello World”

lambda是一种特殊形式，可以用来定义函数，它接收多个参数，第一个参数为函数的参数列表。

在解释器输入 vhello, fhello 都会输出它们的值，说明 Scheme 以统一的方式看待一般数据类型和函数。

定义有参函数

在 lambda 后面声明一个参数列表来定义有参函数，编辑以下代码并保存为 farg.scm:

; hello with name
(define hello
  (lambda (name)
    (string-append "Hello " name "!")))


; sum of three numbers
(define sum3
  (lambda (a b c)
    (+ a b c)))

保存后，就可以加载并调用其中的函数了

(load "farg.scm")
;Loading "farg.scm" -- done
;Value: sum3

(hello "Lucy")
;Value 20: "Hello Lucy!"

(sum3 10 20 30)
;Value: 60

函数定义简洁形式

除 lambda 外，还能用一种更简洁的形式定义函数：

; hello with name
(define (hello name)
  (string-append "Hello " name "!"))


; sum of three numbers
(define (sum3 a b c)
  (+ a b c))

练习1

编写如下简单却实用的函数：

一个将参数+1的函数
一个将参数-1的函数

练习2

略

总结

本章，学习了如何定义函数，特殊形式 define 可以用来定义函数或其他全局参数。下一章，将介绍代码的分支结构

练习答案

练习1

; 1
(define (1+ x)
  (+ x 1))

; 2
(define (1- x)
  (- x 1))

第五章 - 分支

本章内容是关于如何利用条件在程序中产生分支。编写真正实用的程序，分支是必不可少的

if表达式

if 表达式将程序分成两个分支

1	(if predicate then_value else_value)

如果 predicate 为“真”，将计算 then_value 的值，否则，计算 else_value 的值，无论得到哪个值，该值都作为 if 表达式的值。

任何除“假”以外的值都为“真”，以 #t 表示，而“假”以 #f 表示

R5RS标准中定义，#f 和 '() 是两个不同的对象，而在 MIT-Scheme 中，它们是相同的，其参考的是前一个标准 R4RS

所以，不要使用列表作为 predicate。函数 null? 可以判断列表是否为空

(null? '())
;Value: #t

(null? '(a b c))
;Value: ()   ;#f

not 函数可以对 predicate 取反，如果 predicate 为 #f 则得到 #t, 反之则反

if 表达式不对所有参数求值，因此是特殊形式的一种，如果 predicate 为“真”，只有 then_value 会被求值，否则，只有 else_value 会被求值

可以省略 else_value 参数，在这种情况下，如果 predicate 为“假”，求出的值是不确定的。

练习1

编写如下函数：

1
2
3

1. A function to return the absolute value of a real number.
2. A function to return the reciprocal of a real number. Make it return #f if the argument is 0.
3. A function to convert a integer to a graphical character of ASCII characters. The integers that can be converted to graphical characters are 33 – 126. Use integer->char to convert a integer to a character. Make it return #f if the given integer can not be converted to a graphical character.

and和or

and 和 or 均为特殊形式，它们可以组合多个条件，Scheme 中的 and 和 or 与其他语言如 C 不同，Scheme 中的 and 和 or 不返回 #t 或 #f, 而是返回其中一个参数的值。and 和 or 可以让代码变得更短

and

and 接收若干参数，并从左到右求值，如果一个参数的值为 #f，它返回 #f, 其余参数就不求值了。相反，如果所有参数都不为 #f，它返回最后一个参数的值

(and #f 0)
;Value: ()

(and 1 2 3)
;Value: 3

(and 1 2 3 #f)
;Value: ()

or

or 接收若干参数，并从左到右求值，它返回第一个不为 #f 的参数的值, 其余参数就不求值了。如果最后一个参数被求值了，就返回最后一个参数的值。

(or #f 0)
;Value: 0

(or 1 2 3)
;Value: 1

(or #f 1 2 3)
;Value: 1

(or #f #f #f)
;Value: ()

练习2

实现以下函数：

1
2

1. A function that takes three real numbers as arguments. It returns the product of these three numbers if all them is positive.
2. A function that takes three real numbers as arguments. It returns the product of these three numbers if at least one of them is negative.

cond表达式

虽然所有条件都可以用 if 表达，但复杂的条件会让程序看起来过于复杂，针对这种情况，cond 便应运而生。

cond 格式如下：

(cond
  (predicate_1 clauses_1)
  (predicate_2 clauses_2)
    ......
  (predicate_n clauses_n)
  (else        clauses_else))

cond 表达式会从上到下依次求值 predicate_i，如果 predicate_i 为“真”，就会对 clauses_i 求值，并将该值作为 cond 表达式的值，同时停止计算 predicate_i 后面的表达式。

如果所有 predicate_i 都为“假”，cond 表达式的值就取 clauses_else 的值。

可以在每个 clauses_i 的地方编写多个S表达式，而最后一个S表达式的值将成为 clauses_i 的值。

示例：市营游泳池价格

市营游泳池的价格取决于顾客的年龄

free if age ≤ 3 or age ≥ 65.
0.5 dollars for 4 ≤ age ≤ 6.
1.0 dollars for 7 ≤ age ≤ 12.
1.5 dollars for 13 ≤ age ≤ 15.
1.8 dollars for 16 ≤ age ≤ 18.
2.0 dollars for others.

可编写函数计算不同年龄对应的价格：

(define (fee age)
  (cond
   ((or (<= age 3) (>= age 65)) 0)
   ((<= 4 age 6) 0.5)
   ((<= 7 age 12) 1.0)
   ((<= 13 age 15) 1.5)
   ((<= 16 age 18) 1.8)
   (else 2.0)))

练习3

实现如下函数：

The grade (A – D) of exam is determined by the score (score). Write a function that takes a score as an argument and returns a grade.
    A if score ≥ 80
    B if 60 ≤ score ≤ 79
    C if 40 ≤ score ≤ 59
    D if score < 40

构造 predicate 的函数

介绍一些可以构造 predicate 的函数，这种函数的特点是名字以 ? 结尾。

eq?, eqv?, 和equal?

eq?, eqv?, equal?都接受两个参数，并比较它们是否相同，这些函数之间有一些细微差别如下：

eq? 比较两个参数的地址是否相同，如果相同则返回 #t。不要使用 eq? 比较数字，尽管在 MIT-Scheme 里是可以的，但其并没有在 R5RS 中规定，这种情形须使用 eqv?

(define str "hello")
;Value: str

(eq? str str)
;Value: #t

(eq? "hello" "hello")
;Value: ()             ← It should be #f in R5RS 

;;; comparing numbers depends on implementations
(eq? 1 1)
;Value: #t

(eq? 1.0 1.0)
;Value: ()

eqv? 比较存储在内存中两个数据的值及其数据类型，如果两个数据的值和数据类型都相同则返回 #t。用它比较两个过程（lambda 表达式）的结果取决于具体 Scheme 实现。eqv? 不能用于比较序列（如列表和字符串），因为尽管两个序列看起来相同，序列第一个地址存储的内容也是不同的。

(eqv? 1.0 1.0)
;Value: #t

(eqv? 1 1.0)
;Value: ()

;;; don't use it to compare sequences
(eqv? (list 1 2 3) (list 1 2 3))
;Value: ()

(eqv? "hello" "hello")
;Value: ()

;;; the following depends on implementations
(eqv? (lambda(x) x) (lambda (x) x))
;Value: ()

equal? 用于比较两个序列（如列表和字符串）

(equal? (list 1 2 3) (list 1 2 3))
;Value: #t

(equal? "hello" "hello")
;Value: #t

判断数据类型的函数

以下这些是判断数据类型的函数，它们都接受一个参数：

pair? 如果数据是由 cons cell 组成的，返回 #t

list? 如果数据是列表，返回 #t, 注意：’() 是列表但不是pair

null? 如果数据是 ‘()，返回 #t

symbol? 如果数据是符号，返回 #t

char? 判断数据是否是字符

string? 判断数据是否是字符串

number? 判断数据是否是数字

complex? 判断数据是否是复数

real? 判断数据是否是实数

rational? 判断数据是否是分数

integer? 判断数据是否是整数

exact? 判断数据是否不是一个浮点数

inexact? 判断数据是否是一个浮点数

比较数字的函数

=, <, >, <=, >=

这些函数接受若干个参数，如果参数大小顺序符合函数名，函数返回 #t

(= 1 1 1.0)
;Value: #t

(< 1 2 3)
;Value: #t
(< 1)
;Value: #t
(<)
;Value: #t

(= 2 2 2)
;Value: #t

(< 2 3 3.1)
;Value: #t

(> 4 1 -0.2)
;Value: #t

(<= 1 1 1.1)
;Value: #t

(>= 2 1 1.0)
;Value: #t

(< 3 4 3.9)
;Value: ()

odd?, even?, positive?, negative?, zero?

这些函数接受一个参数，如果参数性质符合函数名，则返回 #t

比较字符的函数

char=?, char<?, char>?, char<=?, char>=?

这些函数用于比较字符，访问 R5RS 了解更多

比较字符串的函数

string=?，string-ci=?等

这些函数用于比较字符串，访问 R5RS 了解更多

总结

本章学习了：if 表达式和 cond 表达式可以用来构造分支结构

下一章将学习局部变量

练习答案

练习1

; 1
(define (my-abs n)
  (* n
     (if (positive? n) 1 -1)))
     
; 2     
(define (inv n)
  (if (not (zero? n))
      (/ n)))

; 3
(define (i2a n)
  (if (<= 33 n 126)
      (integer->char n)))

练习2

; 1
(define (pro3and a b c)
  (and (positive? a)
       (positive? b)
       (positive? c)
       (* a b c)))

; 2
(define (pro3or a b c)
  (if (or (negative? a)
	  (negative? b)
	  (negative? c))
      (* a b c)))

练习3

(define (score n)
  (cond
   ((>= n 80) 'A)
   ((<= 60 n 79) 'B)
   ((<= 40 n 59) 'C)
   (else 'D)))

第六章 - 局部变量

前面讲解了如何定义函数，但尚未涉及到如何定义局部变量，这样函数容易产生冗余（译注：不能保存多次相同运算结果）

下面介绍局部变量，它可以使定义复杂函数更轻松

let表达式

可以用 let 表达式定义局部变量，格式如下：

1	(let binds body)

在 binds 表中声明函数并赋初值，body 包含若干个S表达式

binds 表的格式如下：

1	[binds] → ((p1 v1) (p2 v2) ...)

以上声明了 p1, p2 并赋初值 v1, v2, 它们的作用域在 body 内

示例1：定义局部变量 i，j，并赋值为 1，2，然后计算 i+j

1
2
3

(let ((i 1) (j 2))
  (+ i j))
;Value: 3

let 表达式可以嵌套

示例2：定义局部变量 i，j，并赋值为 1, i+2，然后 i，j 相乘

(let ((i 1))
  (let ((j (+ i 2)))
    (* i j)))
;Value: 3

下面的代码无法运行，因为在 i 没有定义在 j 的作用域

1
2
3

(let ((i 1) (j (+ i 2)))
  (* i j))
;Error

let 表达式允许引用同一个 binds 表里定义的变量，实际上， let 表达式是嵌套 let 表达式的一种语法糖

1
2
3

(let* ((i 1) (j (+ i 2)))
  (* i j))
;Value: 3

示例3: quadric-equation 函数计算一元二次方程的根

quadric-equation

1 2	(quadric-equation 3 5 2) ; solution of 3x2+5x+2=0 ;Value 12: (-2/3 -1)

再实际，let 表达式其实是 lambda 表达式的一种语法糖

(let ((p1 v1) (p2 v2) ...) exp1 exp2 ...)
⇒
((lambda (p1 p2 ...)
    exp1 exp2 ...) v1 v2) ; 译注：用 v1，v2 调用了 lambda

总结

本章介绍了 let 表达式，并且提到，let 表达式只是 lambda 表达式的一种语法糖

在 Scheme 中，变量的作用域由 let 表达式或 lambda 表达式定义，作用域通过代码自然地体现出来，这称为语法闭包

接下来，将介绍循环

第七章 - 循环

在 Scheme 中，do 语句可以构造循环，但是，递归也是一种常见“循环”形式

递归

递归函数是一个调用自身的函数，并被常常用来描述循环。

计算阶乘广泛用于认识递归，以下 fact 函数可以计算阶乘：

(define (fact n)
  (if (= n 1)
      1
      (* n (fact (- n 1)))))

通常，递归将使用更多内存空间，而且由于多次函数调用，时间开销也更大

然而，递归函数可以更简单地构建循环。由于列表是被递归地定义的，所以列表和递归能很好地合作

举个例子，以下函数将列表每个元素乘以 2：

(define (list*2 ls)
  (if (null? ls)
      '()
      (cons (* 2 (car ls))
	    (list*2 (cdr ls)))))

练习1

用递归实现以下函数：

1. A function that counts the number of list items, my-length. (Function length is pre-defined.)
2. A function that summarizes numbers in a list.
3. A function that takes a list (ls) and an object (x) as arguments and returns a list removing x from ls.
4. A function that takes a list (ls) and and an object (x) and returns the first position of x in ls. The position is counted from 0. If x is not found in ls, the function returns #f.

尾递归

上面提到，常规递归效率不高。相对的，尾递归函数将本次调用计算结果直接作为下一次调用的参数并直接返回下一次调用结果，这避免了保留当前调用的栈，特别的，Scheme 标准要求在执行前要将尾递归转换为循环，避免了多次函数调用的开销

以下就是计算阶乘的尾递归版本：

(define (fact-tail n)
  (fact-rec n n))

(define (fact-rec n p)
  (if (= n 1)
      p
      (let ((m (- n 1)))
	(fact-rec m (* p m)))))

通过尾递归转换，Scheme 甚至可以不需要专门的循环语法

练习2

用尾递归实现下列函数：

1. my-reverse that reverse the order of list items. (Function reverse is pre-defined.)
2. Summarizing items of a list consisting of numbers.
3. Converting a string that represents a positive integer to the corresponding integer, i.e. "1232" → 1232. Input error check is not required.
Hint:
    1. Character to number conversion is done by subtracting 48 from the ASCII codes of characters #\0 ... #\9. Function char->integer is available to get the ASCII code of a character.
    2. Function string->list is available to convert string to a list of characters.

命名let

命名 let 可用于构建循环，下面的 fact-let 函数显示如何使用命名 let 计算阶乘。

(define (fact-let n)
  (let loop((n1 n) (p n))           ; 1
    (if (= n1 1)                    
	p
	(let ((m (- n1 1)))
	  (loop m (* p m))))))      ; 2

该函数使用了一个命名 let 表达式（loop）以替代之前的 fact-rec。一开始它在 ; 1 标记的地方用 n 初始化参数 (n1, p)。每次循环，每次循环结束，这些参数在 ; 2 标记的地方得到更新：将 n1 减 1，并将 p 乘以 (n1 - 1)

命名 let 是传统构建循环的方法。

译注：依我理解，(let loop((n1 n) (p n)) ...)是定义了一个名为 loop 的函数

练习3

用命名 let 实现以下函数：

1
2
3

1. Questions 3 and 4 of exercise 1.
2. The function of exercise 2.
3. The function range that returns a list of numbers from 0 to n (not including n).

letrec

letrec 和命名 let 相似，但由 letrec 定义的名字可以在定义中可以引用它自己。我们一般用 letrec 定义复杂的递归函数，下面是 letrec 版的 fact 函数：

(define (fact-letrec n)
  (letrec ((iter (lambda (n1 p)
		   (if (= n1 1)
		       p
		       (let ((m (- n1 1)))
			 (iter m (* p m)))))))     ; *
    (iter n n)))

注意看 ‘; *’ 那一行，局部变量 iter 可在自己的定义中引用自己

letrec 语法常用于定义局部函数

练习4

用 letrec 实现练习2中题目

do表达式

do 是不太常用的一种构建循环的方式，它的格式如下：

1 2	(do binds (predicate value) body)

在 binds 处定义变量，如果 predicate 为“真”，就跳出循环然后返回 value，否则，继续循环

binds 部分的格式如下：

1	[binds] → ((p1 i1 u1) (p2 i2 u2) ... )

变量 p1, p2 被初始化为 i1, i2, 每次循环结束被更新为 u1, u2

以下是 do 表达式版本的 fact 函数

1 2	(define (fact-do n) (do ((n1 n (- n1 1)) (p n (* p (- n1 1)))) ((= n1 1) p)))

练习5

用 do 实现练习2中题目

总结

通过目前所学知识，我们已经能用 Scheme 解决常规问题了

下一章，我们学习高阶函数，高阶函数让我们的代码更具 Scheme 风格

练习答案

练习1

; 1
(define (my-length ls)
  (if (null? ls)
      0
      (+ 1 (my-length (cdr ls)))))

; 2
(define (my-sum ls)
  (if (null? ls)
      0
      (+ (car ls) (my-sum (cdr ls)))))

; 3
(define (remove x ls)
  (if (null? ls)
      '()
      (let ((h (car ls)))
        ((if (eqv? x h)
            (lambda (y) y)
            (lambda (y) (cons h y)))
         (remove x (cdr ls))))))
        
; 4
(define (position x ls)
  (position-aux x ls 0))

(define (position-aux x ls i)
  (cond
   ((null? ls) #f)
   ((eqv? x (car ls)) i)
   (else (position-aux x (cdr ls) (1+ i)))))

练习2

; 1
(define (my-reverse ls)
  (my-reverse-rec ls ()))

(define (my-reverse-rec ls0 ls1)
  (if (null? ls0)
      ls1
      (my-reverse-rec (cdr ls0) (cons (car ls0) ls1))))

;-------------------
; 2
(define (my-sum-tail ls)
  (my-sum-rec ls 0))

(define (my-sum-rec ls n)
  (if (null? ls)
      n
      (my-sum-rec (cdr ls) (+ n (car ls)))))

;--------------------
; 3
(define (my-string->integer str)
  (char2int (string->list str) 0))

(define (char2int ls n)
  (if (null? ls)
      n
      (char2int (cdr ls) 
		(+ (- (char->integer (car ls)) 48)
		   (* n 10)))))

练习3

; 1
(define (remove x ls)
  (let loop((ls0 ls) (ls1 ()))
    (if (null? ls0) 
	(reverse ls1)
	(loop
	 (cdr ls0)
          (if (eqv? x (car ls0))
              ls1
            (cons (car ls0) ls1))))))

; 2
(define (position x ls)
  (let loop((ls0 ls) (i 0))
    (cond
     ((null? ls0) #f)
     ((eqv? x (car ls0)) i)
     (else (loop (cdr ls0) (1+ i))))))

; 3
(define (my-reverse-let ls)
  (let loop((ls0 ls) (ls1 ()))
    (if (null? ls0)
	ls1
	(loop (cdr ls0) (cons (car ls0) ls1)))))

; 4
(define (my-sum-let ls)
  (let loop((ls0 ls) (n 0))
    (if (null? ls0)
	n
	(loop (cdr ls0) (+ (car ls0) n)))))

; 5
(define (my-string->integer-let str)
  (let loop((ls0 (string->list str)) (n 0))
    (if (null? ls0)
	n
	(loop (cdr ls0)
	      (+ (- (char->integer (car ls0)) 48)
		 (* n 10))))))

; 6
(define (range n)
  (let loop((i 0) (ls1 ()))
    (if (= i n)
        (reverse ls1)
      (loop (1+ i) (cons i ls1)))))

练习4

; 1
(define (my-reverse-letrec ls)
  (letrec ((iter (lambda (ls0 ls1)
		   (if (null? ls0)
		       ls1
		       (iter (cdr ls0) (cons (car ls0) ls1))))))
    (iter ls ())))

; 2
(define (my-sum-letrec ls)
  (letrec ((iter (lambda (ls0 n)
		   (if (null? ls0)
		       n
		       (iter (cdr ls0) (+ (car ls0) n))))))
    (iter ls 0)))

; 3
(define (my-string->integer-letrec str)
  (letrec ((iter (lambda (ls0 n)
		   (if (null? ls0)
		       n
		       (iter (cdr ls0)
			     (+ (- (char->integer (car ls0)) 48)
				(* n 10)))))))
    (iter (string->list str) 0)))

练习5

; 1
(define (my-reverse-do ls)
  (do ((ls0 ls (cdr ls0)) (ls1 () (cons (car ls0) ls1)))
      ((null? ls0) ls1)))

; 2
(define (my-sum-do ls)
  (do ((ls0 ls (cdr ls0)) (n 0 (+ n (car ls0))))
      ((null? ls0) n)))

; 3
(define (my-string->integer-do str)
  (do ((ls0 (string->list str) (cdr ls0))
       (n 0 (+ (- (char->integer (car ls0)) 48) 
	       (* n 10))))
      ((null? ls0) n)))

第一章 - 安装MIT-Scheme

为何学习Scheme

安装MIT-Scheme

如何在 Windows 安装MIT-Scheme

第二章 - 将 Scheme 作为计算器使用

介绍

将 Scheme 作为计算器使用

四种基本运算

其他算术运算符

商、余数、取模、开方

三角函数

幂和对数

总结

练习答案

第三章 - 列表

Cons Cells与列表

Cons Cells

Lists

Atoms

quote

特殊形式

car函数、cdr函数

list函数

总结

练习答案

第四章 - 定义函数

定义简单函数并加载执行

定义有参函数

函数定义简洁形式

总结

练习答案

第五章 - 分支

if表达式

and和or

and

or

cond表达式

构造 predicate 的函数

eq?, eqv?, 和equal?

判断数据类型的函数

比较数字的函数

比较字符的函数

比较字符串的函数

总结

练习答案

第六章 - 局部变量

let表达式

总结

第七章 - 循环

递归

尾递归

命名let

letrec

do表达式

总结

练习答案

第八章 - 高阶函数

第九章 - 输入/输出

第十章 - 赋值

第十一章 - 字符、字符串

第十二章 - 符号

第十三章 - 关联列表和哈希表

第十四章 - 向量和结构

第十五章 - 定义语法

第十六章 - Continuation

第十七章 - 惰性求值

第十八章 - Nondeterminism